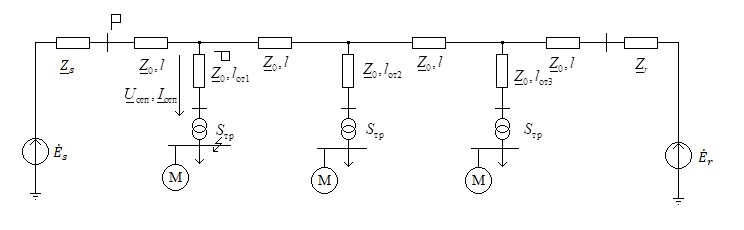
Мы публикуем статьи наших сотрудников с молодежной конференции Академии электротехнических наук Чувашской республики (АЭН ЧР) «Электротехника, электроэнергетика, электромеханика – 2018», в ходе которой были рассмотрены актуальные вопросы развития релейной защиты и автоматизации, например, прозвучал доклад на тему «Алгоритмическая модель длинной линии, как локатор замыкания на землю». Авторы данной статьи являются сотрудники компании Релематика: Чернов А.Ю., Белянин А.А., Лямец Ю.Я.
Аннотация. Рассматривается метод определения места замыкания в сетях среднего напряжения на базе применения разностных уравнений длиной линии путём анализа характеристики распределения напряжения.
Электроэнергетические системы 6-35 кВ, как известно, в большинстве своём работают с режимом изолированной или компенсированной нейтралью в целях уменьшения тока однофазного замыкания на землю (ОЗЗ), т.к. именно этот вид повреждения наиболее распространен на практике. Однако, сложность процессов при ОЗЗ, обусловленная разветвленной конфигурацией сетей, различием в заземлении нейтрали и рядом прочих факторов, привела к тому, что на сегодняшний момент нет надежного средства дистанционного определения мест замыканий на землю.
Цель данной работы заключается в построении простого и точного метода определения места повреждения. Известно, что в условиях металлического замыкания на землю наблюдается снижение напряжения поврежденной фазы до нуля в месте аварии. Следовательно, основой для формирования вывода о месте повреждения может стать поиск нулевых точек на характеристике распределения напряжения.
Особенностью предлагаемого метода является использование мгновенных величин, которые позволяют оперировать точным математическим описанием длинной линии [1] – разностными уравнениями (1), минуя энергозатратное и медленное выделение ортогональных составляющих, используемое в подавляющем большинстве реализаций алгоритмов определения местоположения повреждения.
Участок линии без потерь, представленный на рис. 1, описывается парой уравнений (1), на основе которых может быть построена алгоритмическая модель [2], преобразующая наблюдаемые электрические величины в начале участка в величины произвольного места.
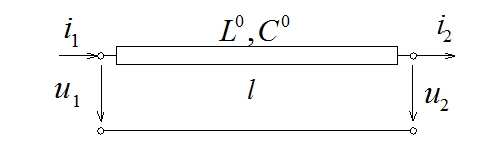
Рис. 1. Модель участка линии без потерь
u1(t) – RBi1(t) = u2(t – τ) – RBi2(t – τ)
(1)
u2(t) + RBi2(t) = u1(t – τ) – RBi1(t – τ)
где RB = √(L0/C0) – волновое сопротивление линии, τ = l√(L0/C0) – время пробега волны вдоль линии, L0, C0 – удельные индуктивность и ёмкость, l – длинна линии.
Таким образом, локация повреждения в данном случае осуществляется в два этапа. На первом этапе по известным данным начала u1 и i1 при помощи алгоритмической модели рассчитывается напряжение u2 в каждой точке линии. На втором этапе строится распределение напряжения вдоль всей длины линии для конкретного момента времени. Из анализа полученной зависимости делается предположение о реальном месте повреждения.
Для проверки предложенного метода в программном комплексе MatLab/Simulink была построена имитационная модель двухфидерной сети, представленная на рис. 2. Параметры модели: линейное напряжение на шинах – 35 кВ, мощность нагрузки Pнг = 30 кВт, линии приняты одинаковыми, удельные параметры линий: R10 = 0,14Ом/км, L10 = мГн/км, C10 = 380 нФ/км, R00 = 0,67 Ом/км, L00 = 4,5 мГн/км, C00 = 400 нФ/км; длина линий l = 20 км. На одном из присоединений в момент времени t = 0,2 с на расстоянии xf = 10 км моделируется однофазное замыкание фазы А на землю через переходное сопротивление Rf. Наблюдаются фазные напряжения на шинах и фазные токи в начале поврежденной линии.
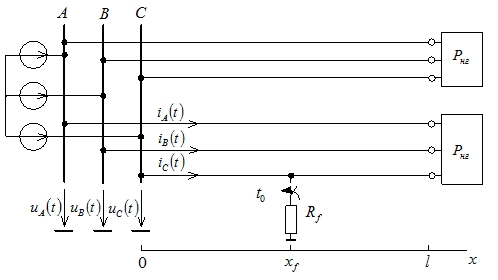
Рис. 2. Имитационная модель сети
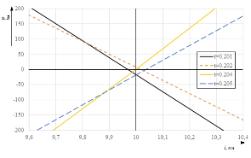
При помощи алгоритмической модели, построение которой подробно описано в [2], строится характеристика распределения напряжения поврежденной фазы вдоль линии для разных моментов времени: через 1,2,4 и 5 мс после возникновения замыкания на землю. На рис. 3 укрупненно приведена область скопления пересечений характеристик с осью абсцисс при металлическом замыкании. Из рисунка видно, что данные пересечения располагаются в непосредственной близости от места реального повреждения (xf = 10 км.).
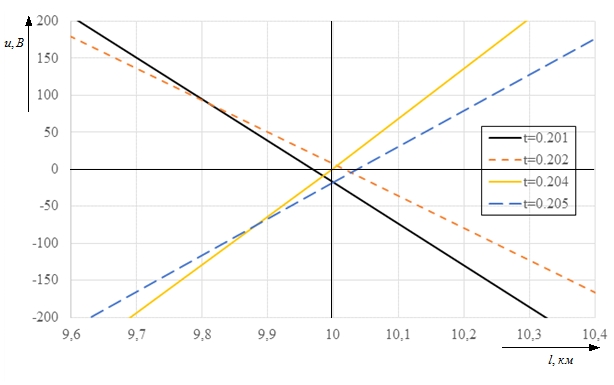
Рис. 3. Характеристика распределения напряжения вдоль линии
Таким образом, полученные результаты подтверждают возможность применения данного способа для локации замыканий на землю.
Выводы
1. Метод обладает значительным быстродействием: локация места повреждения возможна уже через 1-5 мс после его возникновения.
2. Метод характеризуется достаточной точностью: при металлическом замыкании относительная погрешность определения места повреждения составляет порядка 0.06%, при величине переходного сопротивления 0.5 Ом – 1.25%.
Литература
1. Лямец Ю.Я., Белянин А.А., Воронов П.И. Анализ переходных процессов в длинной линии в базисе дискретного и непрерывного времени // Изв. Вузов. Электромеханика. 2012. №4. С. 11 – 16.
2. Лямец Ю.Я., Белянин А.А., Воронов П.И. Алгоритмическое моделирование фидера в переходном режиме // Изв. Вузов. Электромеханика. 2013. №5. С. 49 – 56.