Аннотация: Необходимость скорейшего предотвращения опасных условий работы энергосистемы требует от измерительных органов (ИО) быстродействие срабатывания в режиме короткого замыкания (КЗ) и точность работы во всем диапазоне возможных частот в режиме асинхронного хода. Этим требованиям удовлетворяют измерительные органы, действующие в базисе мгновенных величин. В настоящей работе выполнено сравнение измерений, выполненных с использованием алгоритмических моделей на основе фильтров ортогональных составляющих и мгновенных величин.
Введение
Существующая классификация режимов работы энергосистемы имеет многоступенчатую структуру разделения видов повреждений и ненормальных режимов. В каждом режиме ожидается определенный набор воздействий от устройств релейной защиты и автоматики (РЗА). Точное и своевременное выявление вида режима в заданной точке сети позволяет выполнить скорейшее предотвращение и ликвидацию опасных условий работы энергосистемы. В режиме короткого замыкания (КЗ) требуется быстродействие срабатывания, а в режиме асинхронного хода необходима точная работа измерительных органов защит во всем диапазоне возможных частот и, возможно, блокирование действия отдельных функций РЗА. Этим требованиям удовлетворяют измерительные органы, действующие в базисе мгновенных величин. Использование мгновенных величин позволяет обойти недостатки, присущие цифровым фильтрам ортогональных составляющих.
В работе представлены результаты исследования режима асинхронного хода. Показаны результаты испытания алгоритмической модели, способной «перешагнуть» через элемент электрической сети и предоставить напряжения и токи в заданной точке наблюдения, даны точностные характеристики алгоритмической модели. Приведено сравнение результатов с традиционными измерительными органами на базе фильтров ортогональных составляющих.
Моделирование электрических процессов в линии электропередачи в базисе мгновенных величин
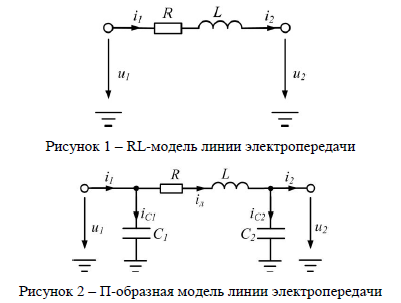
Алгоритмическое моделирование предполагает расчет электрических величин в заданной точке сети на основе определенного набора измерений. Рассмотрим RL-модель линии электропередачи, представленную на рис. 1. Уравнения модели в дискретной форме
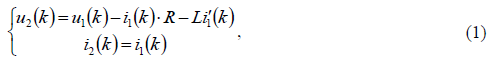
Уравнения (1) могут быть использованы для вычисления напряжения  и тока
и тока  по известным значениям напряжения
по известным значениям напряжения  , тока
, тока  и производной тока
и производной тока  . Один из способов расчета производной тока по времени
. Один из способов расчета производной тока по времени  связан с численным дифференцированием. Производную тока будем определять с применением разностных уравнений [1].
связан с численным дифференцированием. Производную тока будем определять с применением разностных уравнений [1].
Если по линии электропередачи протекает емкостный ток значительной величины, то в модели необходимо дополнительно учесть поперечную емкостную проводимость. На рис. 2 представлена П-образная модель линии.
Добавление в схему элементов емкости означает отбор тока, вычисление которого основано на производной напряжения по времени:
![]()
П-образная модель линии электропередачи содержит три реактивных элемента, ток или напряжение на которых определяются уравнением с производной. Последовательно от «входа» модели к ее «выходу» необходимо решить три дифференциальных уравнения для каждого реактивного элемента. На каждом этапе решения точка замера «сдвигается» на один реактивный элемент ближе к «выходу» модели. Число таких этапов определяет порядок модели. Таким образом, П-образная модель линии электропередачи имеет третий порядок.
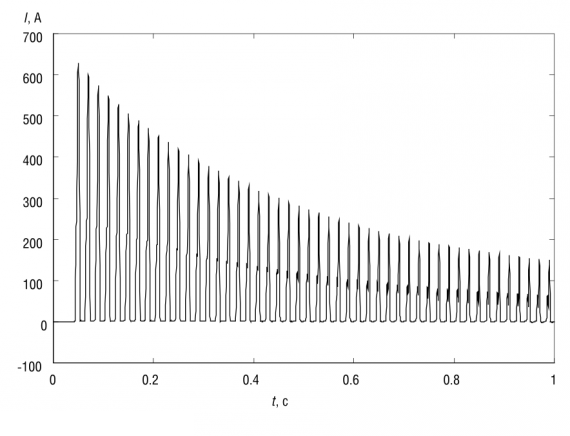
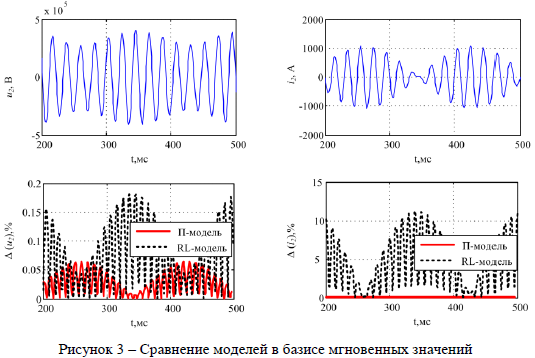
На рис. 3 приведено сравнение осциллограмм напряжения  и тока
и тока  в режиме асинхронного хода (АХ) на линии 500 кВ длиной 100 км, полученных с использованием алгоритмической модели линии (АМО) (RL- или П-образной модели) и измеренных в имитационной модели (ИМО). Входные величины АМО – напряжение
в режиме асинхронного хода (АХ) на линии 500 кВ длиной 100 км, полученных с использованием алгоритмической модели линии (АМО) (RL- или П-образной модели) и измеренных в имитационной модели (ИМО). Входные величины АМО – напряжение  и ток
и ток  в начале линии, измеренные в ИМО. Относительная приведенная погрешность получена по выражению:
в начале линии, измеренные в ИМО. Относительная приведенная погрешность получена по выражению:
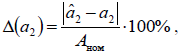
где  – номинальная величина тока или напряжения соотвтетсвенно;
– номинальная величина тока или напряжения соотвтетсвенно; – величина, измеренная в ИМО;
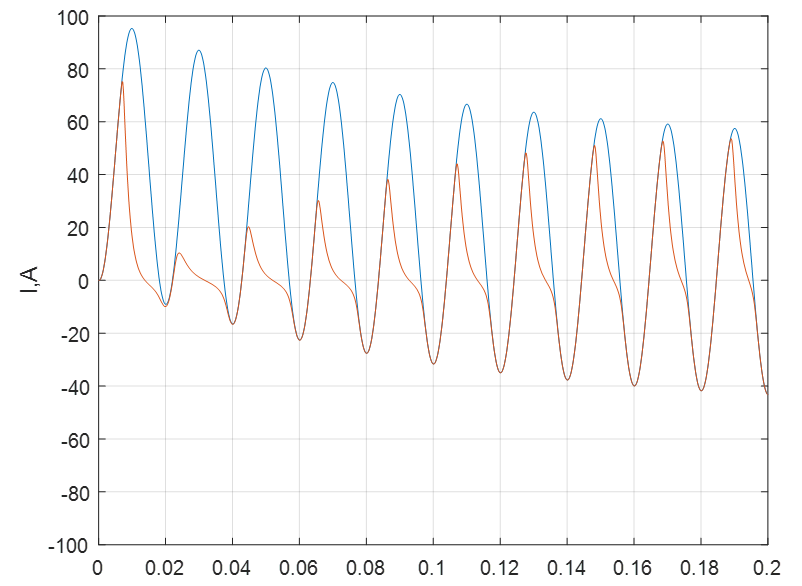
– величина, измеренная в ИМО;  – оценка величины при помощи АМО. RL-модель не учитывает емкостную проводимость линии, что приводит к погрешности расчета тока
– оценка величины при помощи АМО. RL-модель не учитывает емкостную проводимость линии, что приводит к погрешности расчета тока  до 10%, напряжения
до 10%, напряжения  – до 0,2%. Погрешность расчета в П-образной модели достигает 0,03% для
– до 0,2%. Погрешность расчета в П-образной модели достигает 0,03% для  , 0,06% – для
, 0,06% – для  . Осциллограммы погрешностей обнаруживают преимущества П-модели при необходимости определения тока
. Осциллограммы погрешностей обнаруживают преимущества П-модели при необходимости определения тока  . Погрешности в режиме АХ имеют один порядок величины с погрешностями, наблюдаемыми в нагрузочном режиме.
. Погрешности в режиме АХ имеют один порядок величины с погрешностями, наблюдаемыми в нагрузочном режиме.
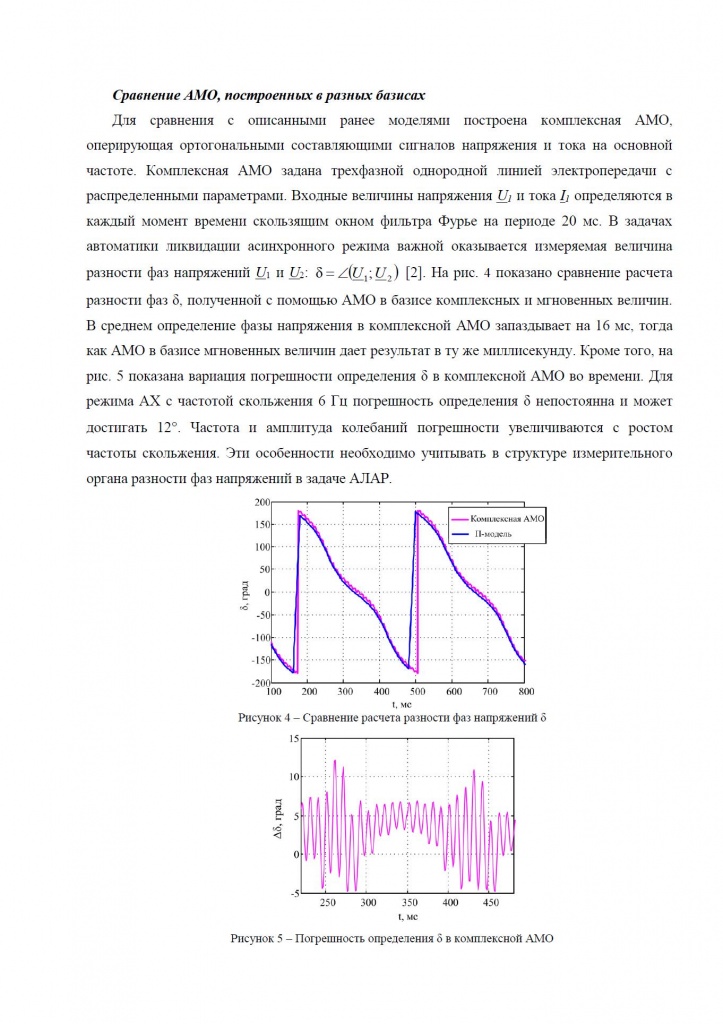
Сравнение АМО, построенных в разных базисах
Для сравнения с описанными ранее моделями построена комплексная АМО, оперирующая ортогональными составляющими сигналов напряжения и тока на основной частоте. Комплексная АМО задана трехфазной однородной линией электропередачи с распределенными параметрами. Входные величины напряжения  и тока
и тока  определяются в каждый момент времени скользящим окном фильтра Фурье на периоде 20 мс. В задачах автоматики ликвидации асинхронного режима важной оказывается измеряемая величина разности фаз напряжений
определяются в каждый момент времени скользящим окном фильтра Фурье на периоде 20 мс. В задачах автоматики ликвидации асинхронного режима важной оказывается измеряемая величина разности фаз напряжений  и
и  :
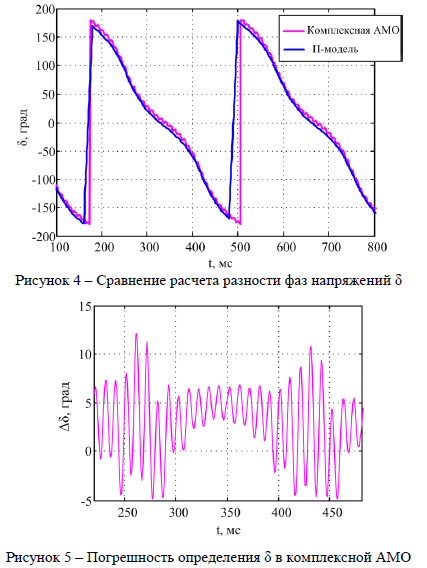
:  [2]. На рис. 4 показано сравнение расчета разности фаз
[2]. На рис. 4 показано сравнение расчета разности фаз  , полученной с помощью АМО в базисе комплексных и мгновенных величин. В среднем определение фазы напряжения в комплексной АМО запаздывает на 16 мс, тогда как АМО в базисе мгновенных величин дает результат в ту же миллисекунду. Кроме того, на рис. 5 показана вариация погрешности определения
, полученной с помощью АМО в базисе комплексных и мгновенных величин. В среднем определение фазы напряжения в комплексной АМО запаздывает на 16 мс, тогда как АМО в базисе мгновенных величин дает результат в ту же миллисекунду. Кроме того, на рис. 5 показана вариация погрешности определения  в комплексной АМО во времени. Для режима АХ с частотой скольжения 6 Гц погрешность определения δ непостоянна и может достигать 12
в комплексной АМО во времени. Для режима АХ с частотой скольжения 6 Гц погрешность определения δ непостоянна и может достигать 12 . Частота и амплитуда колебаний погрешности увеличиваются с ростом частоты скольжения. Эти особенности необходимо учитывать в структуре измерительного органа разности фаз напряжений в задаче АЛАР.
. Частота и амплитуда колебаний погрешности увеличиваются с ростом частоты скольжения. Эти особенности необходимо учитывать в структуре измерительного органа разности фаз напряжений в задаче АЛАР.
Выводы
В работе представлены результаты исследования способа алгоритмического моделирования линий электропередачи в базисе мгновенных величин в условиях асинхронного режима. Расчеты показали, что погрешность моделирования напряжения удаленного конца линии при использовании RL- или П-образной модели удовлетворительная и не превышает 0,2% даже при значительном отклонении напряжения и тока от номинальной частоты. Выявлено, что АМО на основе фильтров ортогональных составляющих имеет запаздывание на 16 мс и погрешность до 12 относительно имитационной модели в режиме АХ.
относительно имитационной модели в режиме АХ.
Список литературы
- Турчак Л.И. Основы численных методов / Л.И. Турчак, П.В. Плотников – М.: Физматлит, 2002. – 304 с.
- Наровлянский В.Г. Современные методы и стредства предотвращения асинхронного режима электроэнергетической системы / В.Г. Наровлянский – М.: Энергоатомиздат, 2004. – 360 с.