Каскадная алгоритмическая модель линии электропередачи в базисе мгновенных величин

Аннотация: Необходимость скорейшего предотвращения опасных условий работы энергосистемы требует от измерительных органов (ИО) быстродействие срабатывания в режиме короткого замыкания (КЗ) и точность работы во всем диапазоне возможных частот в режиме асинхронного хода. Этим требованиям удовлетворяют измерительные органы, действующие в базисе мгновенных величин. В настоящей работе представлены результаты разработки каскадной алгоритмической модели объекта (АМО).

Введение

Существующая классификация режимов работы энергосистемы имеет многоступенчатую структуру разделения видов повреждений и ненормальных режимов. В каждом режиме ожидается определенный набор воздействий от устройств релейной защиты и автоматики (РЗА). Точное и своевременное выявление вида режима в заданной точке сети позволяет выполнить скорейшее предотвращение и ликвидацию опасных условий работы энергосистемы. В режиме короткого замыкания (КЗ) требуется быстродействие срабатывания, а в режиме асинхронного хода необходима точная работа измерительных органов защит во всем диапазоне возможных частот и, возможно, блокирование действия отдельных функций РЗА. Этим требованиям удовлетворяют измерительные органы, действующие в базисе мгновенных величин. Использование мгновенных величин позволяет обойти недостатки, присущие цифровым фильтрам ортогональных составляющих.

В работе представлены результаты разработки алгоритмической каскадной модели объекта (АМО). Описаны принципы построения такой модели с учетом особенностей базиса мгновенных величин.

Моделирование электрических процессов в линии электропередачи в базисе мгновенных величин

Алгоритмическое моделирование предполагает расчет электрических величин в заданной точке сети на основе определенного набора измерений. Рассмотрим RL-модель линии электропередачи, представленную на рис. 1. Уравнения модели в дискретной форме 

u₂(k) = u₁(k) – i₁(k) · R – Li′₁(k)
                                                                           (1)
i₂(k) = i₁(k)

Уравнения (1) могут быть использованы для вычисления напряжения u₂ и тока i₂ по известным значениям напряжения u₁, тока i₁ и производной тока i′₁. Один из способов расчета производной тока по времени i′₁связан с численным дифференцированием с применением разностных уравнений [1]

i′₁(k) = i₁(k+1) – i₁(k–1) / T_d           (2)

где T_d – период дискретизации.

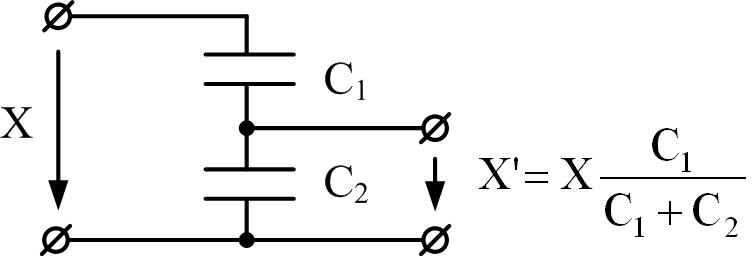
Если по линии электропередачи протекает емкостный ток значительной величины, то в модели необходимо дополнительно учесть поперечную емкостную проводимость. На рис. 2 представлена П-образная модель линии.

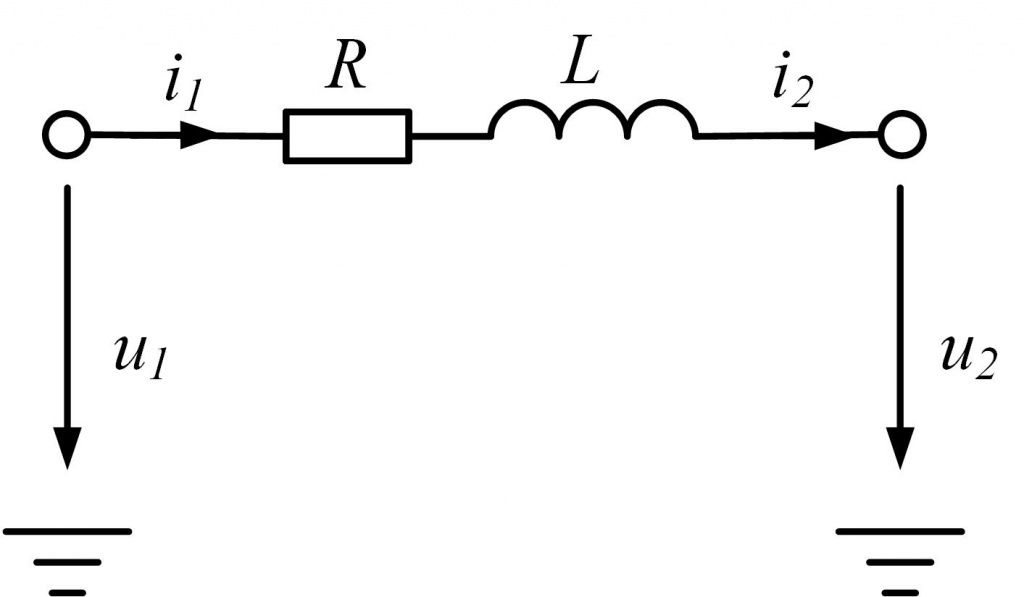
Рис. 1 – RL-модель линии электропередачи

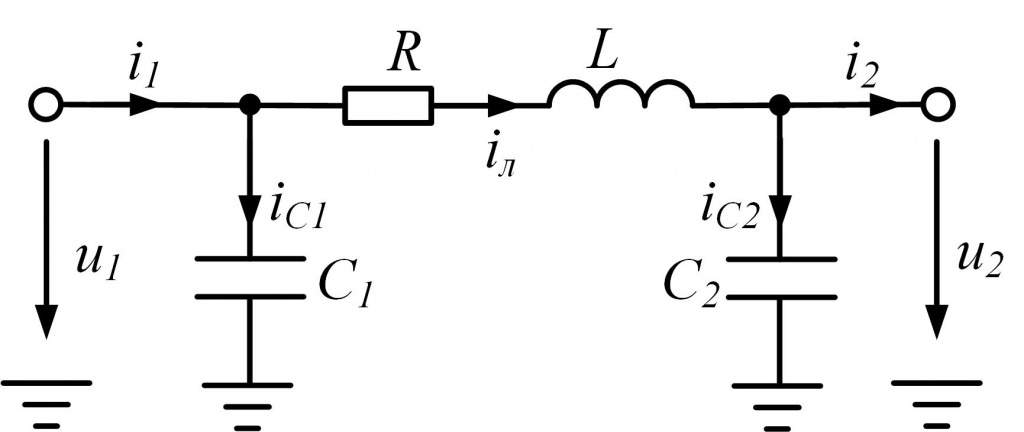
Рис. 2 – П-образная модель линии электропередачи

Добавление в схему элементов емкости означает отбор тока, вычисление которого основано на производной напряжения по времени:

i_c(k) = Cu'(k)     (3)

П-образная модель линии электропередачи содержит три реактивных элемента, ток или напряжение на которых определяются уравнением с производной. Последовательно от «входа» модели к ее «выходу» необходимо решить три дифференциальных уравнения для каждого реактивного элемента. На каждом этапе решения точка замера «сдвигается» на один реактивный элемент ближе к «выходу» модели. Число таких этапов определяет порядок модели. Таким образом, П-образная модель линии электропередачи имеет третий порядок.

Каскадная алгоритмическая модель линии электропередачи в базисе мгновенных величин

Алгоритмическая модель объекта (АМО) используется в решении задачи определения величин тока и напряжения в заданной точке сети на основе измерений в фиксированной точке наблюдения. Эта заданная точка сети может быть отделена от точки наблюдения на некоторое количество звеньев, описанных уравнениями (1)-(3). Задача описания принципов  объединения этих звеньев решается в этом разделе.

Из методов информационной теории РЗА известен метод каскадного эквивалентирования цепей [2], который применим только для составляющих основной гармоники. Аналогичного метода для базиса мгновенных величин не существует, но свойства этого метода целесообразно было бы использовать для каскадного соединения АМО в базисе мгновенных величин. На рис. 3 показан принцип каскадного соединения АМО.

Само понятие «каскадная» по отношению к модели предполагает, что выход одного звена модели является входом для другого. Сопряжение звеньев АМО должно выполняться с помощью линейных матричных операций над передаточными функциями звеньев. Передаточные функции звеньев записываются в виде матрицы передачи в форме В

u₂(k)            U₁(l)
  = B · 
i₂(k)             I₁(l)

где В – коэффициенты матрицы передачи формы В для одного звена каскада, записанные на основе уравнений (1)-(3);

U₁(l), I₁(l) – векторы выборок тока и напряжения в месте фиксированного наблюдения;

u₂(k), i₂(k) – текущие отсчеты напряжения и тока на выходе звена.

Порядок матричных операций должен соответствовать порядку следования соответствующих звеньев АМО. Каждая последующая операция должна оптимальным способом связать выход (n-1)-го звена со входом n-го звена. В результате должна получиться эквивалентная матрица передачи B_экв, которая будет связывать текущие отсчеты тока и напряжения в заданной точке сети с выборками тока и напряжения в месте фиксированного наблюдения.

Полученная таким образом каскадная АМО будет иметь ограничения, связанные с выбором способа расчета производной. При выборе способа необходимо учесть 2 фактора: чем шире окно наблюдения производной, тем выше точность расчета производной; чем меньше окно наблюдения производной, тем меньше запаздывание расчета тока и напряжения на выходе АМО [3]. Исходя из этого, возможно, потребуется повышение частоты дискретизации измерения тока и напряжения в месте наблюдения.

Увеличение количества звеньев кратно увеличивает запаздывание на расчет АМО. Также количество всех звеньев ограничивается необходимой точностью расчета тока (напряжения) на выходе АМО.

Рис. 3 – АМО радиального участка линии с числом звеньев, равным n

Выводы

В работе представлены результаты разработки каскадной алгоритмической модели объекта. Обоснована необходимость ее разработки. Описаны принципы построения такой модели с учетом особенностей базиса мгновенных величин. Указаны ограничения полученной модели.

Литература

• Турчак Л.И. Основы численных методов / Л.И. Турчак, П.В. Плотников – М.: Физматлит, 2002. – 304 с.
• Лямец Ю.Я., Шевелев А.В., Еремеев Д.Г. Каскадное эквивалентирование статических энергообъектов. – Вестник Чувашского университета, 2004, №2, с.160-169
• Подшивалин А.Н., Михайлов М.В. Алгоритмическое моделирование в базисе мгновенных величин в условиях асинхронного режима // Труды АЭН ЧР. №1. 2018. С. 41-44.